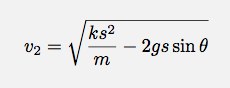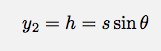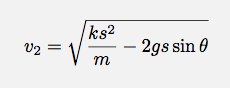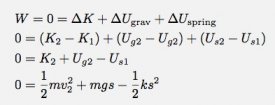Over analyze the motion of Angry Birds.
Excerpt:
Does the Bird’s Launch Speed Depend on the Angle?
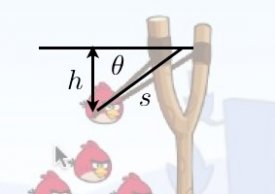
If the bird is indeed shot from an elastic cord, then technically the bird should go faster when shot horizontally than when it is shot straight up. Why? Physics. Let me draw a diagram for a bird that is shot straight up. Also, let me assume that this sling shot is just a spring.
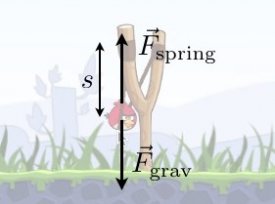
Let me assume a spring with a spring constant k and a bird mass of m. How do I find an expression for how fast it will be when it leaves the sling shot? Yes, use the work-energy principle. Why? Because I know the starting and ending positions, but I don’t know the time. Since work-energy doesn’t use time, it is a perfect fit.
I will let the Earth + bird + slingshot be my system and it will start at y1 = 0 meters and end at y2 = s. Since I have the Earth and the slingshot both in my system, I can have both gravitational potential energy and spring potential energy. Oh, let me point out that the bird starts from rest and there is no work done on the system. The work-energy principle would say:
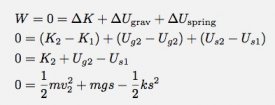
Maybe it wasn’t clear, but the spring potential energy is (1/2)ks2 and the gravitational potential energy is mgy. Now, I can solve for the final velocity:
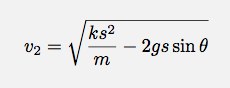
Excerpt:
Does the Bird’s Launch Speed Depend on the Angle?
If the bird is indeed shot from an elastic cord, then technically the bird should go faster when shot horizontally than when it is shot straight up. Why? Physics. Let me draw a diagram for a bird that is shot straight up. Also, let me assume that this sling shot is just a spring.

Let me assume a spring with a spring constant k and a bird mass of m. How do I find an expression for how fast it will be when it leaves the sling shot? Yes, use the work-energy principle. Why? Because I know the starting and ending positions, but I don’t know the time. Since work-energy doesn’t use time, it is a perfect fit.
I will let the Earth + bird + slingshot be my system and it will start at y1 = 0 meters and end at y2 = s. Since I have the Earth and the slingshot both in my system, I can have both gravitational potential energy and spring potential energy. Oh, let me point out that the bird starts from rest and there is no work done on the system. The work-energy principle would say:
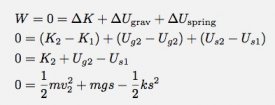
Maybe it wasn’t clear, but the spring potential energy is (1/2)ks2 and the gravitational potential energy is mgy. Now, I can solve for the final velocity: